Le problème
Comment fait-on quand on ne trouve pas un algorithme élégant qui solutionne mathématiquement un problème, en donnant une solution parfaite ? On transige, en bon développeur pragmatique…
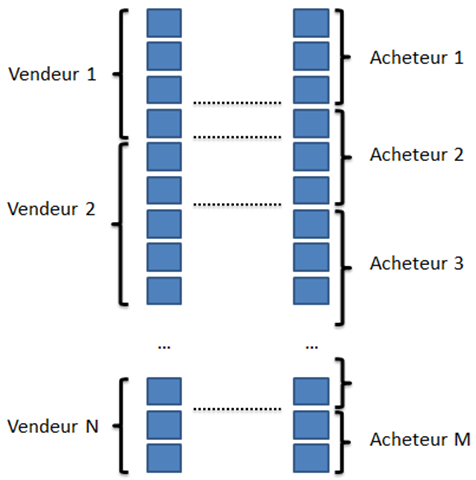
Prenons le cas d’un échange de titres dans le cadre d’un rachat des actions d’une société. Imaginons que nous ayons N vendeurs possédant chacun un nombre entier d’actions, et M acheteurs, souhaitant acheter chacun un nombre entier d’actions, le total des actions vendues étant évidemment égal au total des actions achetées.
Si on aligne bêtement les vendeurs et les acheteurs, on voit sur l’exemple ci-dessus qu’il faudrait un échange de trois actions entre le vendeur 1 et l’acheteur 1, puis d’une action entre le vendeur 1 et l’acheteur 2, deux entre le vendeur 2 et l’acheteur 2, etc.
D’instinct, en mettant dans l’ordre des plus gros détenteurs et des plus gros vendeurs respectivement, on se dit qu’on doit pouvoir réduire le nombre de chèques échangés, mais ça n’a rien d’une réelle optimisation, car il suffit d’un décalage d’une seule action pour mettre par terre tout un bel alignement.
Par contre, il y a peut-être un algorithme pour aligner correctement, mais perso, je ne suis pas un crack en maths, et j’ai eu beau retourner ça dans ma tête pendant quelques heures, je n’ai pas trouvé la recette miracle.
Le principe
Du coup, on va passer à un autre mode d’optimisation, pas parfaite, mais avec de bonnes chances de tomber sur un optimum relatif. De toute façon, on n’est pas à un échange prêt, seule la précision sur les nombres d’actions est importante. Ensuite, s’il y a un ou deux échanges de plus que l’optimal absolu, pas grave… Bref, algorithmes génétiques à la rescousse !
L’idée des algorithmes génétiques est de simuler une optimisation séquentielle en codant les solutions dans des chromosomes, et en réalisant l’équivalent d’une évolution naturelle, à savoir que les solutions qui ont le plus de valeur (dans notre cas, qui nécessitent le moins d’échanges de chèques) seront favorisées pour apparaitre dans la prochaine génération (qui correspond à l’itération). Ces solutions favorisées se croiseront pour produire des solutions qui seront encore meilleures, et dans ce cas elles poursuivront l’évolution, ou bien moins bonnes et elles laisseront la place aux autres.
Après quelques itérations, on voit en général une stabilisation des solutions. Si on a bien réglé le calcul, les solutions trouvées sont assez proches de l’optimum. Toute la difficulté dans les algorithmes génétiques est de faire en sorte de ne pas étouffer la diversité génétique : il faut donc un algorithme de sélection qui secoue bien les gènes et créent des chromosomes suffisamment différents pour que certains soient meilleurs que leurs ancêtres. Mais il faut bien sûr équilibrer avec une fonction permettant de trier les meilleurs chromosomes, et c’est le rôle de la fonction d’évaluation (souvent appelée fitness) qui est utilisée pour supprimer les chromosomes les moins adaptés.
L’outillage
Mais passons à la pratique. Nous allons pour cela commencer par créer un projet de test dans Visual Studio :
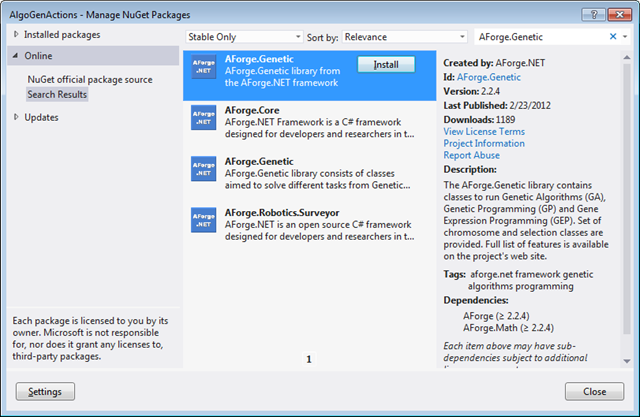
Puis, nous utiliserons le gestionnaire de références pour ajouter la librairie AForge.Genetic ainsi que ses références. C’est beaucoup plus simple avec NuGet qu’auparavant…
Choix du chromosome et du codage
La première chose à faire avant de coder est de réfléchir à la façon de faire tenir l’information nécessaire aux algorithmes génétiques sur un chromosome. Dans notre cas, c’est relativement simple : AForge fournit un chromosome de base de type ShortArrayChromosome, qui embarque un tableau d’entiers. Nous allons donc utiliser le début pour stocker l’ordre des vendeurs et la seconde pour stocker l’ordre des acheteurs. Dans notre exemple, nous allons prendre 10 vendeurs et 32 acheteurs, et nous aurons donc besoin d’un chromosome avec 42 entrées :
using System; using Microsoft.VisualStudio.TestTools.UnitTesting; using AForge.Genetic; namespace AlgoGenActions { [TestClass] public class UnitTest1 { [TestMethod] public void TestMethod1() { IChromosome IndividuRacine = new ShortArrayChromosome(42); } } }
Attention, ce chromosome contient bien l’ordre des vendeurs et acheteurs, et non pas le nombre d’actions que possèdent ou veut acheter chacun. Ce nombre est fixe par personne, et ne servira que lors du calcul de la valeur de la solution portées par le chromosome.
Création de la fonction d’évaluation
Justement, c’est la fonction d’évaluation (ou fitness) qui va gérer ceci. Pour commencer, nous créons une classe pour implémenter AForge.Genetic.IFitnessFunction :
class FitnessRepartitionActions : IFitnessFunction { public double Evaluate(IChromosome chromosome) { throw new NotImplementedException(); } }
Avant même de se poser la question de la méthode de calcul (eh oui… il va quand même falloir qu’on fasse un peu d’algorithmes, sinon ce ne serait pas marrant), il faut qu’on donne le nombre d’actions de chaque vendeur et acheteur :
ushort[] Vendeurs = new ushort[] { 911, 612, 712, 276, 520, 491, 280, 110, 134, 1 }; ushort[] Acheteurs = new ushort[] { 48, 48, 320, 250, 115, 110, 253, 665, 69, 10, 412, 82, 30, 30, 30, 150, 30, 300, 100, 35, 30, 60, 70, 60, 350, 30, 50, 100, 30, 30, 150 };
L’étape d’après consiste, dans la fonction Evaluate, à récupérer l’état du chromosome courant :
ushort[] genes = ((ShortArrayChromosome)chromosome).Value;
Les 12 premiers gènes représentent l’ordre des vendeurs. Nous allons nous en servir pour créer la liste ordonnée des nombres d’actions vendues. L’algorithme est un peu spécial, car le contenu des gènes n’est pas comme on le souhaiterait un numéro de vendeur, garantissant qu’il ne sera pas répété. Chaque gène peut prendre n’importe quelle valeur de ushort, y compris des valeurs similaires, alors qu’un même vendeur ne vend pas deux fois ses actions.
Il nous faut donc un mécanisme un peu spécial qui commence par ramener le ushort à la taille de l’offset maximum pour cibler le prochain vendeur, c’est-à-dire le nombre de vendeurs décrémenté d’une unité, puis utiliser un tableau stockant les positions restant disponibles pour être sûr de ne pas dupliquer l’information. Au final, ça donne ceci :
int NBVENDEURS = Vendeurs.Length; int[] positionsVendeurs = new int[NBVENDEURS]; List<int> positionsRestantes = Enumerable.Range(0, NBVENDEURS).ToList(); for (int i = 0; i < NBVENDEURS; i++) { ushort gene = genes[i]; int offset = gene % (NBVENDEURS - i); positionsVendeurs[i] = positionsRestantes[offset]; positionsRestantes.RemoveAt(offset); } ushort[] vendeursOrdonnes = new ushort[NBVENDEURS]; for (int i = 0; i < NBVENDEURS; i++) vendeursOrdonnes[i] = Vendeurs[positionsVendeurs[i]];
On n’oublie pas bien sûr d’ajouter les deux using qui vont bien :
using System.Collections.Generic; using System.Linq;
L’étape suivante consiste à répéter exactement le même code pour obtenir la liste ordonnée des actions achetées. Puis, on peut passer au calcul de fitness proprement dit. Là, c’est relativement simple : on compte simplement le nombre de frontières totales, c’est-à-dire les passages d’un vendeur à l’autre ou d’un acheteur au suivant, en ne comptant simplement pas les cas où ça tombe pile. Bref, on compte le nombre de lignes en pointillés sur le premier schéma tout en haut de cet article.
List<int> frontieresActions = new List<int>(); ushort cumulActions = 0; for (int i = 0; i < NBVENDEURS; i++) { cumulActions += vendeursOrdonnes[i]; frontieresActions.Add(cumulActions); } cumulActions = 0; for (int i = 0; i < NBACHETEURS; i++) { cumulActions += acheteursOrdonnes[i]; if (!frontieresActions.Contains(cumulActions)) frontieresActions.Add(cumulActions); }
Il ne nous reste plus alors qu’à renvoyer un double entre 0 et 1, sachant que plus le nombre est haut, plus le chromosome évalué porte une solution intéressante. Pour cela, on utilise une simple fonction affine inversant le nombre de frontières. En effet, plus celui-ci est élevé, moins la solution portée par le chromosome est bonne.
En théorie, le nombre minimal de chèques est égal à Max(N, M), tandis que le nombre maximal est certainement autour de deux fois ce nombre minimal (peut-être décrémenté d’une unité…). On peut donc écrire le code ci-dessous :
double Valeur = 2.0 - (1.0 / Math.Max(NBVENDEURS, NBACHETEURS)) * frontieresActions.Count; return Math.Max(0, Math.Min(1, Valeur));
La classe de fitness est terminée.
Création de la fonction de sélection
Pour compléter les deux faces des algorithmes génétiques, il faut, en plus de la fonction de fitness, une fonction de sélection, c’est-à-dire une méthode qui va créer une nouvelle population à partir d’une ancienne, en brassant les gènes pour essayer de faire apparaître des individus plus adaptés.
Il existe des fonctions de sélection standards qui sont fournies avec AForge.Genetic, comme EliteSelection ou RouletteSelection, mais nous proposons ici d’utiliser une fonction spécialisée qui mélange un peu ces deux comportements :
class RouletteEliteSelection : ISelectionMethod { public void ApplySelection(List<IChromosome> chromosomes, int size) { // On commence par reprendre systématiquement le meilleur chromosome List<IChromosome> NouvelleGeneration = new List<IChromosome>(); double BestFitness = 0.0; foreach (IChromosome Chromosome in chromosomes) BestFitness = Math.Max(BestFitness, Chromosome.Fitness); IChromosome MeilleurChromosome = chromosomes.Find(delegate(IChromosome Chromosome) { return Chromosome.Fitness == BestFitness; }); NouvelleGeneration.Add(MeilleurChromosome); double TotalDesFitness = 0.0; chromosomes.ForEach(delegate(IChromosome Chromosome) { TotalDesFitness += Chromosome.Fitness; }); // Ensuite, on choisit au hasard le reste de la population, en donnant d'autant // plus de chance d'appartenir à la nouvelle génération que la fitness est élevée. Random Generateur = new Random(DateTime.Now.Second + DateTime.Now.Millisecond); while (--size > 0) { double PositionHasard = Generateur.NextDouble() * TotalDesFitness; double FitnessCumulee = 0.0; foreach (IChromosome Chromosome in chromosomes) { FitnessCumulee += Chromosome.Fitness; if (FitnessCumulee > PositionHasard) { NouvelleGeneration.Add(Chromosome); break; } } } chromosomes.Clear(); chromosomes.AddRange(NouvelleGeneration); } }
Cette classe n’est peut-être pas le top de ce qu’on peut faire, car elle ne fait pas de croisement, et n’empêche pas de reprendre plusieurs fois le même chromosome, mais elle ne fonctionne au final pas trop mal. Pour les résultats finaux (voir plus bas), on utilisera plutôt une simple EliteSelection, qui au moins est validée. Bref, je la fais plus voir pour expliquer ce qu’on peut faire, mais si on veut vraiment la mettre en oeuvre en production, il vaudrait mieux la valider fortement, ou au moins la réécrire en fonction de fonctions elles-mêmes déjà validées.
Lancement
Revenons à notre méthode de tests. Il nous faut créer un objet représentant la population de chromosome, ou en termes plus techniques le génome souhaité :
Population Population = new Population(100, IndividuRacine, new FitnessRepartitionActions(), new RouletteEliteSelection());
Cette population porte le nombre de chromosomes à générer par itération, le chromosome que nous avions défini au départ qui sert de clone de base, plus une instance de la classe de fitness, et enfin une instance du mécanisme de sélection que nous avons créée également. Nous pouvons ensuite passer à l’exécution proprement dite, en utilisant le code ci-dessous :
int Iteration = 0; ShortArrayChromosome Meilleur = null; while (Iteration++ < 500) { Population.RunEpoch(); Meilleur = (ShortArrayChromosome)Population.BestChromosome; }
A la fin de l’exécution des tests, on espère avoir une fitness pour la meilleure solution trouvée après les 500 itérations sur 100 chromosomes d’au moins 70% :
Assert.IsTrue(Meilleur.Fitness > 0.7);
On pourrait jouer sur quelques paramètres des algorithmes génétiques, mais il se trouve que leur valeur par défaut est très bien ajustée dans notre cas simple d’utilisation :
//Population.AutoShuffling = false; //Population.CrossoverRate = 0.01; //Population.MutationRate = 0.01; //Population.RandomSelectionPortion = 0.5;
Voila : le programme est prêt à tourner. Vous pouvez le récupérer dans sa version complète à partir de ce lien.
Résultats
Le test passe correctement, avec une fitness de 84% au final. Attention, la partie aléatoire constitutive des algorithmes génétiques fait que vous pouvez trouver une fitness différente au final.
L’évolution de la fitness peut être suivie en modifiant légèrement le code comme ceci :
// Boucle sur les époques de la population int Iteration = 0; ShortArrayChromosome Meilleur = null; using (StreamWriter Scribe = new StreamWriter(@"resultats.csv")) { while (Iteration++ < 500) { Population.RunEpoch(); Meilleur = (ShortArrayChromosome)Population.BestChromosome; Scribe.WriteLine(Meilleur.Fitness); } }
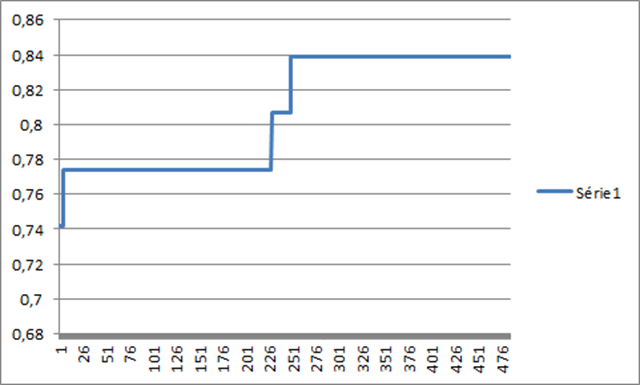
Le résultat ressemble alors à :
Cette évaluation correspond à une petite quarantaine de chèques à échanger, soit une belle optimisation par rapport aux 64 chèques en théorie si on n’avait pas cherché à ordonner les acheteurs sur les vendeurs.
En espérant que ça vous donne envie d’essayer les algorithmes génétiques, qui sont relativement simples à mettre en place, et permettent de se sortir de situations compliquées à peu de frais.